Pythagorean Theorem When Given C

Pythagoras Theorem (also called Pythagorean Theorem) is an important topic in Mathematics, which explains the relation betwixt the sides of a right-angled triangle. The sides of the right triangle are also called Pythagorean triples. The formula and proof of this theorem are explained here with examples.

Pythagoras theorem is basically used to discover the length of an unknown side and the angle of a triangle. By this theorem, we can derive the base of operations, perpendicular and hypotenuse formulas. Let us larn the mathematics of the Pythagorean theorem in detail here.

Table of Contents:

Statement
Formula
Proof
Applications
Problems

Pythagoras Theorem Statement

Pythagoras theorem states that "In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides". The sides of this triangle have been named Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle xc°. The sides of a correct triangle (say a, b and c) which have positive integer values, when squared, are put into an equation, also called a Pythagorean triple.

History

The theorem is named afterward a Greek Mathematician chosen Pythagoras.

Pythagoras Theorem Formula

Consider the triangle given in a higher place:

Where "a" is the perpendicular,

"b" is the base,

"c" is the hypotenuse.

According to the definition, the Pythagoras Theorem formula is given equally:

Hypotenuse ² = Perpendicular ^two + Base ⁱⁱ

c ² = a ² + b ²

The side opposite to the right angle (90°) is the longest side (known as Hypotenuse) considering the side opposite to the greatest bending is the longest.

Pythagoras Theorem

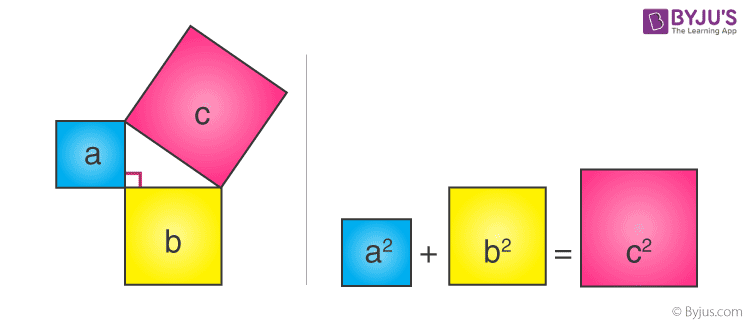
Consider iii squares of sides a, b, c mounted on the 3 sides of a triangle having the aforementioned sides as shown.

By Pythagoras Theorem –

Expanse of square "a" + Surface area of square "b" = Surface area of square "c"

Instance

The examples of theorem and based on the statement given for correct triangles is given below:

Consider a right triangle, given below:

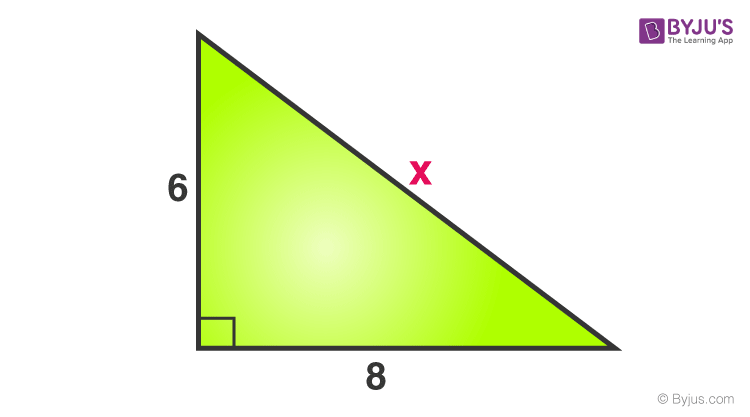
Pythagoras theorem example

Find the value of x.

X is the side opposite to the correct angle, hence it is a hypotenuse.

Now, by the theorem we know;

Hypotenuse ^two = Base ² + Perpendicular ²

x ⁱⁱ = viii ^two + vi ²

ten ² = 64+36 = 100

x = √100 = 10

Therefore, the value of 10 is ten.

Pythagoras Theorem Proof

Given: A right-angled triangle ABC, right-angled at B.

To Evidence- Air-conditioning² = AB² + BC²

Construction: Draw a perpendicular BD meeting Air-conditioning at D.

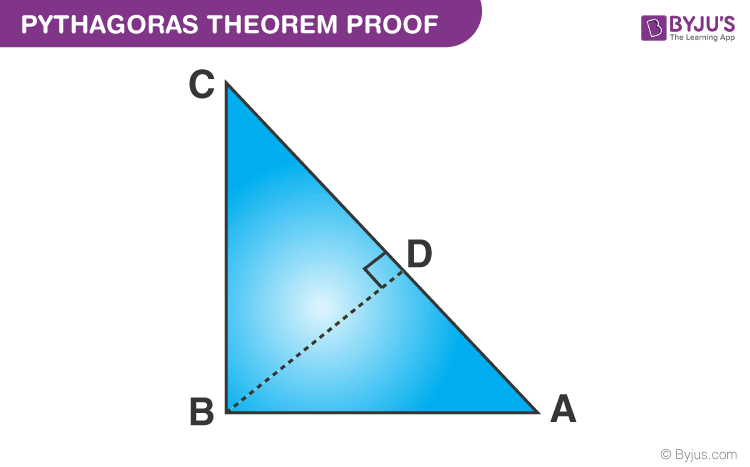
Pythagoras theorem Proof

Proof:

We know, △ADB ~ △ABC

Therefore,

\(\begin{array}{50}\frac{Advertizement}{AB}=\frac{AB}{AC}\cease{assortment} \)

(corresponding sides of like triangles)

Or, ABⁱⁱ= Advertizing × Ac ……………………………..……..(1)

Also, △BDC ~△ABC

Therefore,

\(\brainstorm{array}{l}\frac{CD}{BC}=\frac{BC}{Ac}\end{array} \)

(corresponding sides of similar triangles)

Or, BC²= CD × Ac ……………………………………..(2)

Adding the equations (1) and (2) nosotros get,

ABⁱⁱ+ BC²= AD × AC + CD × AC

AB^two+ BC²= AC (AD + CD)

Since, AD + CD = AC

Therefore, Ac² = AB^two + BCⁱⁱ

Hence, the Pythagorean theorem is proved.

Annotation:Pythagorean theorem is simply applicable to Right-Angled triangle.

Video Lesson on Pythagoras Theorem

Applications of Pythagoras Theorem

To know if the triangle is a correct-angled triangle or not.
In a right-angled triangle, we tin calculate the length of whatever side if the other two sides are given.
To detect the diagonal of a square.

Useful For

Pythagoras theorem is useful to notice the sides of a right-angled triangle. If we know the two sides of a right triangle, and then we can detect the tertiary side.

How to use Pythagoras Theorem?

To utilise Pythagoras theorem, remember the formula given below:

c ² = a ^two + b ²

Where a, b and c are the sides of the right triangle.

For instance, if the sides of a triangles are a, b and c, such that a = three cm, b = 4 cm and c is the hypotenuse. Observe the value of c.

We know,

c ⁱⁱ = a ² + b ²

c ² = three ⁱⁱ +4 ²

c ² = 9+16

c ² = 25

c = √25

c = five cm

Hence, the length of hypotenuse is 5 cm.

How to find whether a triangle is a right-angled triangle?

If we are provided with the length of iii sides of a triangle, then to find whether the triangle is a right-angled triangle or non, we need to employ the Pythagorean theorem.

Let usa understand this statement with the help of an case.

Suppose a triangle with sides 10cm, 24cm, and 26cm are given.

Clearly, 26 is the longest side.

It besides satisfies the condition, 10 + 24 > 26

We know,

c ^two = a ⁱⁱ + b ² ………(1)

So, let a = x, b = 24 and c = 26

First nosotros will solve R.H.Due south. of equation i.

a ² + b ⁱⁱ = 10 ⁱⁱ + 24 ^two = 100 + 576 = 676

Now, taking 50.H.S, nosotros get;

c ² = 26 ² = 676

We tin can see,

LHS = RHS

Therefore, the given triangle is a right triangle, as it satisfies the Pythagoras theorem.

Converse of Pythagoras Theorem
Correct Angle Triangle Theorem
Types Of Triangles
Pythagorean Triples
Right Triangle Congruence Theorem

Pythagorean Theorem Solved Examples

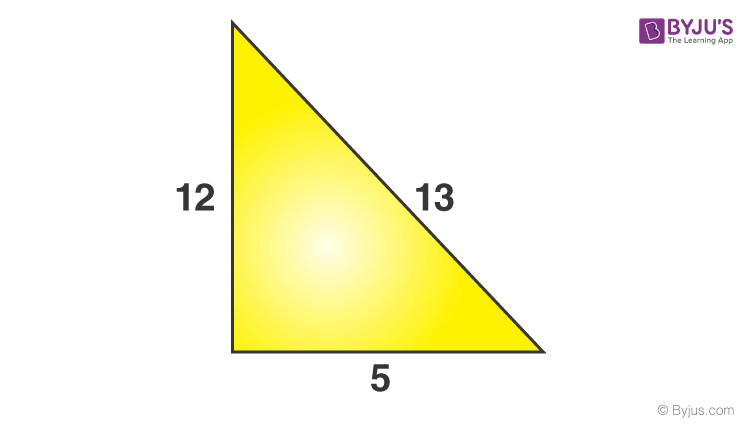
Problem 1:The sides of a triangle are v, 12 & 13 units. Check if information technology has a correct angle or not.

Solution: From Pythagoras Theorem, we accept;

Perpendicular² + Base² = Hypotenuse²

P² + B² = H²

Let,

Perpendicular (P) = 12 units

Base (B)= 5 units

Hypotenuse (H) = 13 units {since it is the longest side measure out}

LHS = P² + B²

⇒ 12² + vⁱⁱ

⇒ 144 + 25

⇒169

RHS = H²

⇒ xiii²

⇒ 169

⇒ 169 = 169

50.H.Due south. = R.H.S.

Therefore, the angle opposite to the 13 units side will exist a right angle.

Pythagoras theorem-problem 1

Problem 2:The two sides of a right-angled triangle are given as shown in the figure. Find the 3rd side.

Solution:Given;

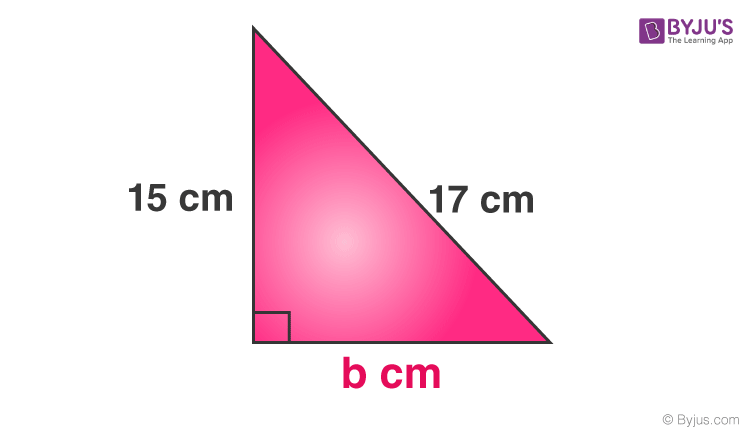
Perpendicular = 15 cm

Base = b cm

Hypotenuse = 17 cm

Every bit per the Pythagorean Theorem, we have;

Perpendicular² + Base of operations^two = Hypotenuse²

⇒15^two + b² = 17²

⇒225 + b² = 289

⇒b² = 289 – 225

⇒b^two = 64

⇒b = √64

Therefore, b = 8 cm

Problem three: Given the side of a square to be 4 cm. Discover the length of the diagonal.

Solution-Given;

Sides of a foursquare = 4 cm

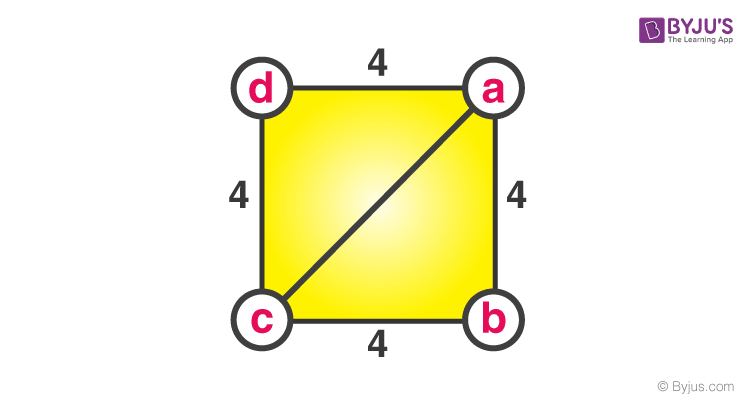
Pythagoras Theorem-problem 3

To Discover- The length of diagonal ac.

Consider triangle abc (or can besides be acd)

(ab)² +(bc)ⁱⁱ= (air-conditioning)²

(four)^two +(4)²= (ac)²

sixteen + 16 = (ac)ⁱⁱ

32 = (air conditioning)²

(air-conditioning)ⁱⁱ = 32

ac = iv√two.

Thus, the length of the diagonal is4√2 cm.

Stay tuned with BYJU'South – The Learning App to larn all the important mathematical concepts and also watch interactive videos to learn with ease.

Oftentimes Asked Questions on Pythagoras Theorem

What is the formula for Pythagorean Theorem?

The formula for Pythagoras, for a right-angled triangle, is given by; P² + B^two = H²

What does Pythagoras theorem state?

Pythagoras theorem states that, in a right triangle, the square of the hypotenuse is equal to the sum of the foursquare of the other two sides.

What is the formula for hypotenuse?

The hypotenuse is the longest side of the right-angled triangle, contrary to right angle, which is adjacent to base and perpendicular. Let base of operations, perpendicular and hypotenuse be a, b and c respectively. So the hypotenuse formula, from the Pythagoras statement volition be;
c = √(a ² + b ⁱⁱ)

Can we use the Pythagoras Theorem for any triangle?

No, this theorem is applicable just for the correct-angled triangle.

What is the use of Pythagoras theorem?

The theorem can be used to find the steepness of the hills or mountains. To find the distance betwixt the observer and a bespeak on the ground from the tower or a building above which the observer is viewing the point. It is generally used in the field of construction.

Tin can the diagonals of a foursquare be found using Pythagoras theorem?

Yes, the diagonals of a square can be plant using the Pythagoras theorem, as the diagonal divides the square into correct triangles.

Explain the steps involved in finding the sides of a correct triangle using Pythagoras theorem.

Step i: To observe the unknown sides of a right triangle, plug the known values in the Pythagoras theorem formula.
Pace two: Simplify the equation to discover the unknown side.
Footstep three: Solve the equation for the unknown side.

What are the different ways to show Pythagoras theorem?

There are various approaches to bear witness the Pythagoras theorem. A few of them are listed below:
Proof using similar triangles
Proof using differentials
Euclid's proof
Algebraic proof, and then on.